一様なライフゲームの統計的性質３

生存／死滅のセルの定義

ライフゲームの挙動を観察すると，不規則な動きのある部分と静止，または周期的な振動する部分に分かれていることがわかる．この不規則な挙動を示す箇所を生存している（Alive），静止・振動の部分を死滅している（Dead）と呼ぶことにする．

以下の１，２，３のいずれか場合のセルを死滅していると定義する．死滅でないセルを生存していると定義する

1. 自セルおよび周囲８セルが全てfalse
2. ２ステップ連続で自セルおよび周囲８セルが同じ値をとる
3. 自セルおよび周囲８セルが周期２の振動を２サイクルする

過去の状態を参照して生存か死滅を決定する．条件２の場合は２ステップ，条件３の場合は４ステップを参照する．周期３以上は，ほとんど存在しないので無視することにする．

また，過去の状態を参照するため，死んだ状態になってから判別するまでに遅れが生じる．条件１の場合は，その傾向を防止し，生存と死滅の境界を明確にするためである．前々回に示した動画は条件１を加えていない．

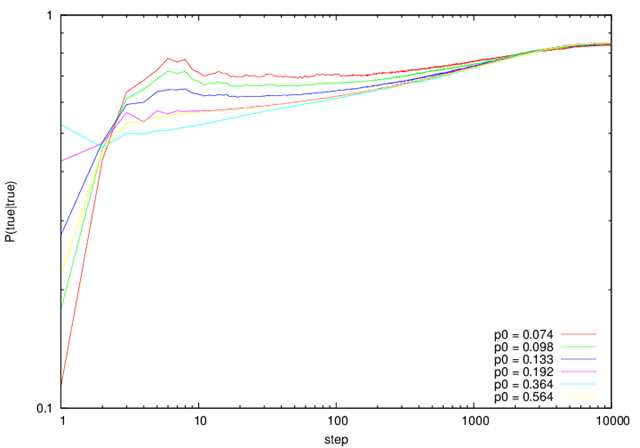
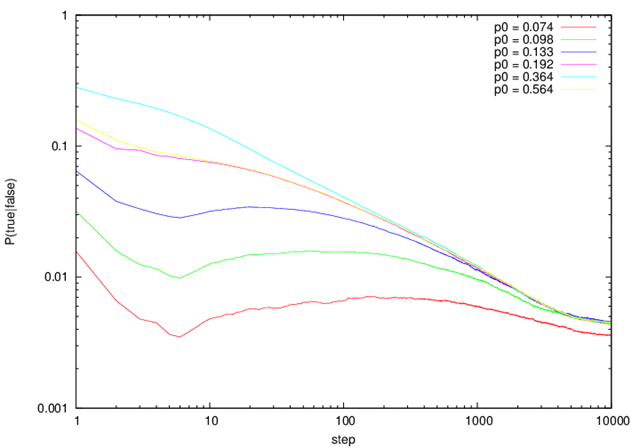
例として，以下のGIFアニメを示す．赤・ピンクが生存するセル．白・黒が死滅したセルでる．赤・黒がtrue，ピンク・白がfalseである．不規則な挙動を示す場所を区別できていることが分かる．

---

条件

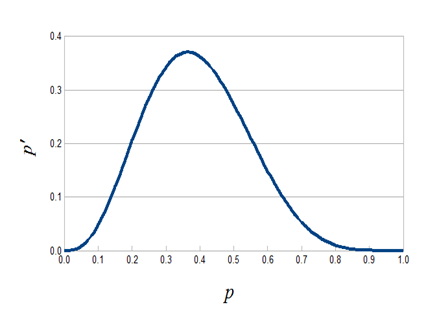
セル数は8192x8192とした．初期条件は確率p0=0.364でtrueとなるような乱数を一様に与えた．

---

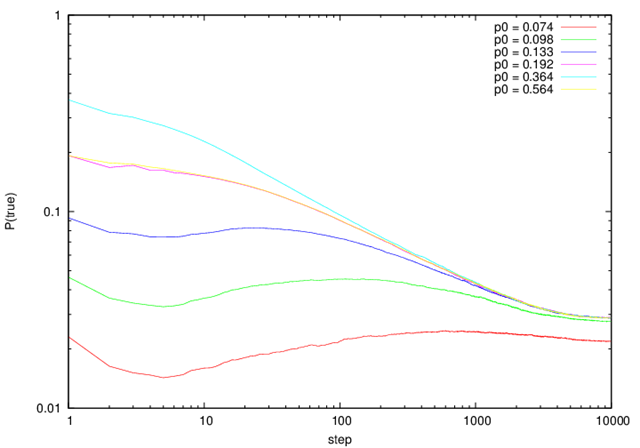
生存のセルの割合の時間変化

以下に生存のセルの割合の時間変化を示す．横軸は前回示したグラフとは異なり，対数軸とはなっていない．

時間とともに生存セルは減少してゆく．とくに，２０００ステップから１００００ステップにて10^(-2.5E-4 x step)に比例して減少していることがわかる．この範囲では，ステップ毎に一定の確率でセルが死滅してゆく．この事実は，ライフゲームの挙動を統計的に議論できることを示している．

図１　生存のセルの割合の時間変化

---

追記　6/23/2013

p0=0.192の場合も追加した．対数グラフなので，8000ステップから異なった値をとっているように見えるが，10^-4のオーダーしか異ならないので実際にはほとんど一緒である．

一様なライフゲームの統計的性質２

条件

初期条件として，確率p0=0.074, 0.098, 0.133, 0.192, 0.364, 0.564でtrueとなる7ケースの一様な乱数を与えたときの挙動について調べてみる．

領域の大きさは4096x4096で，境界は周期境界条件とする．乱数にはc++のrand関数を用いた．貧弱な乱数かもしれないが，特に問題ないだろう．

---

真のセルの確率の変化

図１は真のセルの確率P(true)の時間変化である．

p0=0.192の場合は前回示したように，もしライフゲームが完全にランダムな挙動をするのであれば一定値をとる．しかし，ライフゲームではP(true)は時間と共に減っていき，約10000ステップで定常となる．

また，p0=0.564の場合は，１ステップでのP(true)（以後p1と呼ぶ）がp0=0.192のときと一致するように選んだ値である．両者は互いに一致する．したがって，一様な乱数の初期条件を与えても，密度以外の影響はないといえる．

p0=0.133, 0.192, 0.364, 0.564の場合は時間とともにP(true)は漸近していく．初期のP(ture)が大きい場合初期条件の影響は時間と共に失われていくことがわかる．p0=0.098, 0.074の場合も他の場合に近づいていく傾向にあるが，一致する以前に定常状態に達してしまう．

p0=0.074, 0.098, 0.133は一旦減少したのち，増加する．これらも初期条件の影響が時間と共に失われて，一般的な状態に近づく結果と思われる．

図１　真のセルの確率

---

一様ライフゲームの４つの挙動モード

一様ライフゲームの時間的に変化する挙動を４つのフェーズに分類する．

1. 立ち上がり
2. 漸近
3. 普遍
4. 定常

立ち上がり

立ち上がりは初期の分布の影響が強く現れている状態である．ランダムな初期条件を与えたが，ライフゲームではそのような状態になることはない．初期のランダムな状態は，ライフゲームにおいては「不自然」な状態なのである．そのため，数ステップを要して「自然」な状態に遷移する．

図２，図３は，それぞれ真および偽のセルのが次のステップで真になる確率P(true|true), P(true|false)である．とくにp0が小さい場合に顕著に現れているように，６ステップまでが立ち上がりフェーズである．

p0=0.192, 0.564は立ち上がりフェーズで値が異なっている．この２ケースはp1の値が一致するようにp0を選んだものである．p1が一致していても，分布の傾向は当然異なっている．しかし，立ち上がりフェーズによりこの２ケースの差異は吸収されてしまう．

漸近・普遍

立ち上がりのモードの後はp0=0.364のケースに漸近していく．p1が大きいケースほど早くp0=0.364と一致する．p0=0.364はp1が最大となるケースである．つまり，p0=0.364のケースが最も早く普遍フェーズに遷移し，p1が大きいケースから順に普遍フェーズに遷移していく．

普遍フェーズがどのような状態かは定かではないが，ライフゲームの一般的な性質をもつ状態と予想される．P(true)の変化曲線がべき乗則にしたがい始めた以降の部分が普遍フェーズである．

遷移フェーズとは，立ち上がりフェーズの後，普遍フェーズに遷移するまでの状態である．p1が小さいケース（p0=0.074）は漸近フェーズから普遍フェーズに遷移することなしに次の定常フェーズに遷移してしまう．

定常

定常フェーズとは，すべてのセルが一定値または周期的な挙動をするようなった，つまり死んだ状態になったフェーズである．どのケースでも約10000ステップで定常フェーズに達する．漸近・普遍フェーズから定常フェーズに突然達するわけではない．徐々に死んだセルが増えていき，すべてのセルが死んだときを定常フェーズと呼んでいる．したがって，普遍フェーズも定常フェーズに漸近しているのだが，便宜上，漸近と普遍フェーズの呼び方を区別している．

図2　真のセルから真のセルになる確率

図3　偽のセルから真のセルになる確率

一様なライフゲームの統計的性質１

ライフゲームとは

ライフゲームとは２次元セルオートマトンの一つであり，生命の繁殖死滅を模したシミュレーションモデルである．自らの値cと周囲８セルを参照として，以下のように次ステップでの値c’が決定される．s2は周囲8セルでtrueの値のセルが2，s3は3であることを示す．

この法則にしたがって時間ステップを進めて行くと，下の動画のようなうねうねとした興味深い挙動を示す．赤色のセルは変化の起こっているセル，すなわち生きているセルを示しているが，それについては今後述べていく．

ライフゲームの性質は，過去によく調べられている．しかし，グライダーやブリンカーといった具体的なパターンを見つけるものが多く，統計的な性質についてはあまり知られていないようである．そこでちょっと調べてみようと思う．

一様でランダムなときの挙動

あるステップで，一様に確率pでtrueのとなるような分布をしているとき，次ステップがtrueとなる確率p’は

となる．グラフに示すと以下のようになる．

特徴的な点は次の4点である．p’が最大値をとるp=(14-sqrt(115))/9=0.364，およびp=p’となるp=0.0, 0.192, 0.370である．

もし，分布がつねに一様でランダムであり，上式にしたがってtrueのセルの密度（確率）が変化するとすると，以下のグラフのように数ステップで密度はp=0かp=0.37に漸近する．p(0)=0.192の場合のみ例外でp=0.192を保つ．

もちろん実際のライフゲームでは上記のようにはならない．そこにライフゲームというものの特徴が現れているのである．今後，実際のライフゲームがどのような性質を持っているかを統計的に議論していく．