一様なライフゲームの統計的性質２

条件

初期条件として，確率p0=0.074, 0.098, 0.133, 0.192, 0.364, 0.564でtrueとなる7ケースの一様な乱数を与えたときの挙動について調べてみる．

領域の大きさは4096x4096で，境界は周期境界条件とする．乱数にはc++のrand関数を用いた．貧弱な乱数かもしれないが，特に問題ないだろう．

---

真のセルの確率の変化

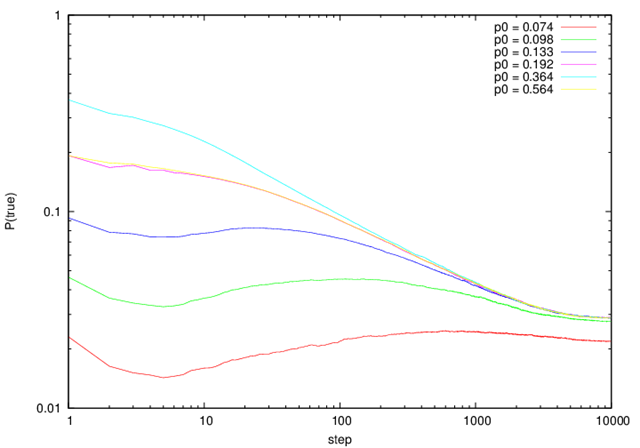
図１は真のセルの確率P(true)の時間変化である．

p0=0.192の場合は前回示したように，もしライフゲームが完全にランダムな挙動をするのであれば一定値をとる．しかし，ライフゲームではP(true)は時間と共に減っていき，約10000ステップで定常となる．

また，p0=0.564の場合は，１ステップでのP(true)（以後p1と呼ぶ）がp0=0.192のときと一致するように選んだ値である．両者は互いに一致する．したがって，一様な乱数の初期条件を与えても，密度以外の影響はないといえる．

p0=0.133, 0.192, 0.364, 0.564の場合は時間とともにP(true)は漸近していく．初期のP(ture)が大きい場合初期条件の影響は時間と共に失われていくことがわかる．p0=0.098, 0.074の場合も他の場合に近づいていく傾向にあるが，一致する以前に定常状態に達してしまう．

p0=0.074, 0.098, 0.133は一旦減少したのち，増加する．これらも初期条件の影響が時間と共に失われて，一般的な状態に近づく結果と思われる．

図１　真のセルの確率

---

一様ライフゲームの４つの挙動モード

一様ライフゲームの時間的に変化する挙動を４つのフェーズに分類する．

1. 立ち上がり
2. 漸近
3. 普遍
4. 定常

立ち上がり

立ち上がりは初期の分布の影響が強く現れている状態である．ランダムな初期条件を与えたが，ライフゲームではそのような状態になることはない．初期のランダムな状態は，ライフゲームにおいては「不自然」な状態なのである．そのため，数ステップを要して「自然」な状態に遷移する．

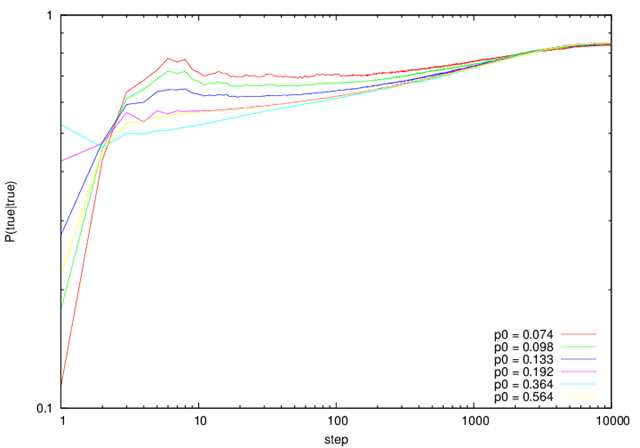
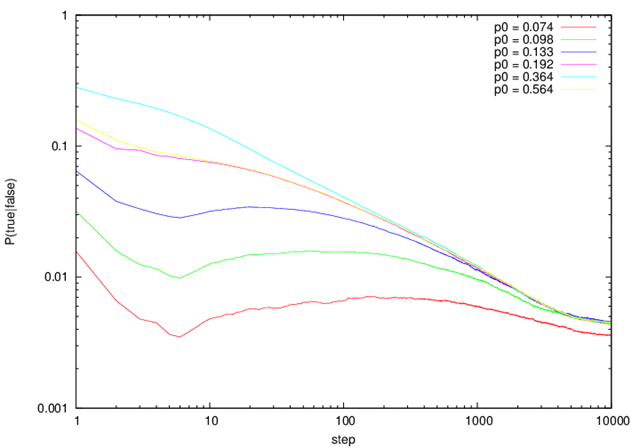
図２，図３は，それぞれ真および偽のセルのが次のステップで真になる確率P(true|true), P(true|false)である．とくにp0が小さい場合に顕著に現れているように，６ステップまでが立ち上がりフェーズである．

p0=0.192, 0.564は立ち上がりフェーズで値が異なっている．この２ケースはp1の値が一致するようにp0を選んだものである．p1が一致していても，分布の傾向は当然異なっている．しかし，立ち上がりフェーズによりこの２ケースの差異は吸収されてしまう．

漸近・普遍

立ち上がりのモードの後はp0=0.364のケースに漸近していく．p1が大きいケースほど早くp0=0.364と一致する．p0=0.364はp1が最大となるケースである．つまり，p0=0.364のケースが最も早く普遍フェーズに遷移し，p1が大きいケースから順に普遍フェーズに遷移していく．

普遍フェーズがどのような状態かは定かではないが，ライフゲームの一般的な性質をもつ状態と予想される．P(true)の変化曲線がべき乗則にしたがい始めた以降の部分が普遍フェーズである．

遷移フェーズとは，立ち上がりフェーズの後，普遍フェーズに遷移するまでの状態である．p1が小さいケース（p0=0.074）は漸近フェーズから普遍フェーズに遷移することなしに次の定常フェーズに遷移してしまう．

定常

定常フェーズとは，すべてのセルが一定値または周期的な挙動をするようなった，つまり死んだ状態になったフェーズである．どのケースでも約10000ステップで定常フェーズに達する．漸近・普遍フェーズから定常フェーズに突然達するわけではない．徐々に死んだセルが増えていき，すべてのセルが死んだときを定常フェーズと呼んでいる．したがって，普遍フェーズも定常フェーズに漸近しているのだが，便宜上，漸近と普遍フェーズの呼び方を区別している．

図2　真のセルから真のセルになる確率

図3　偽のセルから真のセルになる確率