車輪の再発明である.混相流の計算をしている人は経験的に知っていることだが,体系的に調べたものを見たことがなかったので,必要だから計算した.TeXで書いて,PDFにしたのがこちらにある.PDFの方が読みやすいと思う.
水面波の計算における離散化の影響
計算の安定性
差分法を用いて時間発展型の方程式を数値的に解くとき,陽解法の場合,安定した計算を行うためには,格子幅Δに対して,時間刻みΔtに上限があることが知られている.移流方程式でのCourant数uΔt/Δ<1(CFL条件)や,拡散方程式での拡散数DΔt/Δ^2<0.5などが有名である.uは流速,Dは拡散係数である.しかし,水面波の計算を行う際には,これらの条件を満たしていても計算が不安定となる場合があり,別の条件が必要とされる.そこで,微小振幅波の場合に,von Neumannの安定性解析法を適用し,計算の安定性について検証する.
ここに,u=(u,v,w),P,ρはぞれぞれ流体の速度,重力ポテンシャルを含んだ圧力,流体の密度である.
Eular方程式は非線形項を含むため,von Neumannの安定性解析法を適用できない.そこで速度が充分小さいとして非線形項を消去した以下の式について検討する.
上式より,
が成立する.
境界条件は,水深が十分深く,水位変動ηが微小とすると,
となる.g,γは,それぞれ重力加速度,表面張力を密度で割った値である.
空間x,y方向,時間tに関して離散化し,計算することを考える.z方向には離散化を行わない.x,y方向の格子間隔をそれぞれΔx,Δy,時間刻みをΔtとする.x=lΔx,y=mΔy,t=nΔtの差分点での,u,v,w,P,ηの値をそれぞれ,
空間差分にレギュラ格子系,コロケート格子系,スタガード格子系を用いた場合について調べ,差分の方法による違いについて検討を行う.また,水位変動の時間発展にEuler陽解法,2次精度Adams-Bashforce法を用いた場合について調べ,時間発展の方法による違いについて検討する.
となる.離散化された境界条件は,
となる.
u^n_{l,m},v^n_{l,m},w^n_{l,m},P^n_{l,m},η^n_{l,m}を以下のようにFourier級数展開し,波数ごとの安定性を調べていく.
とする.波数k_x,k_yのFourier係数の方程式は以下のようになる.
上からそれぞれ式(1),(2),(3),(4),(5),(6),(7)とする.
式(1),(2),(3),(4)より,
として,
境界条件(4)(5)より,
である.
式(3)(7)より,
となる.
とおくと,
となる.
α,βを
と定義すると,H^nに関する漸化式は以下のように書き換え
られる.
計算の安定条件はすべての波数k_x,k_yに対して|α|<1かつ
|β|<1となることである.
B^2-1<0の場合,α,βは複素数なので,
となり,計算は安定である.B^2-1>0の場合,B>1のとき,α>1,B<-1のとき,β< -1となるので計算は不安定である.したがって,計算が安定となるのはすべての波数k_x,k_yについてB^2-1<0が成立するときである.
Δを
と定義する.BはK_1=K_2=0のとき,最大値
をとり,K_1 = 2/Δ,K_2 = 1/(2Δ)のとき,最小値
をとる.
したがって,安定条件は
である.整理すると,
となる.
レギュラ格子系の場合
速度の離散化をレギュラ格子系にて行った場合には,離散化された支配方程式は,となる.離散化された境界条件は,
となる.
u^n_{l,m},v^n_{l,m},w^n_{l,m},P^n_{l,m},η^n_{l,m}を以下のようにFourier級数展開し,波数ごとの安定性を調べていく.
上からそれぞれ式(1),(2),(3),(4),(5),(6),(7)とする.
式(1),(2),(3),(4)より,
として,
境界条件(4)(5)より,
である.
式(3)(7)より,
となる.
とおくと,
となる.
α,βを
と定義すると,H^nに関する漸化式は以下のように書き換え
られる.
計算の安定条件はすべての波数k_x,k_yに対して|α|<1かつ
|β|<1となることである.
B^2-1<0の場合,α,βは複素数なので,
となり,計算は安定である.B^2-1>0の場合,B>1のとき,α>1,B<-1のとき,β< -1となるので計算は不安定である.したがって,計算が安定となるのはすべての波数k_x,k_yについてB^2-1<0が成立するときである.
Δを
と定義する.BはK_1=K_2=0のとき,最大値
をとり,K_1 = 2/Δ,K_2 = 1/(2Δ)のとき,最小値
をとる.
したがって,安定条件は
である.整理すると,
となる.
コロケート格子系の場合
コロケート格子系の場合は,連続の式の離散化の方法が変わる.レギュラ位置からスタガード位置に速度を補間したものを用いて連続の式を評価する.2次精度のコロケート格子系で離散化された連続の式は,
となり,等間隔直交格子の場合はレギュラ格子系と全く等価である.
したがって,計算の安定条件はレギュラ格子系の場合と同様,
となる.
となり,等間隔直交格子の場合はレギュラ格子系と全く等価である.
したがって,計算の安定条件はレギュラ格子系の場合と同様,
となる.
スタガード格子系の場合
速度の離散化をスタガード格子系にて行った場合には,離散化された支配方程式は,となる.境界条件はレギュラ格子系と同様となる.
Fourier係数の方程式は,
となる.
として,H^nに関する漸化式は
となる.
同様の議論により,計算の安定条件は
となる.
スタガード格子系の場合は,レギュラ格子系およびコロケート格子系の場合と比べ
て,計算が安定となる時間刻みΔtの限界が1/2倍となる.
レギュラ格子系およびコロケート格子系では,1回微分を差分近似する際,2Δx離れた点での差分を取る.一方で,スタガード格子系では,1回微分を差分近似する際,Δx離れた点での差分を取る.したがって,実質の解像度はスタガード格子系の方が1/2の細かさであり,時間刻みは1/2の大きさでなければならない.
Adams-Bashforce法の場合
水位変動の時間発展に以下のような2次精度のAdams-Bashforce法を用いた場合について考える.H^nに関する漸化式は,レギュラ格子系およびコロケート格子系の場合は,
となる.
同様の議論により,安定条件はレギュラ格子系およびコロケート格子系の場合,
,スタガード格子系の場合,
となる.水位変動の時間発展に2次精度のAdams-Bashforce法を用いた場合の条件は,Eular陽解法を用いた場合と同じである.
根号がついた項は波長πΔの水面波の伝播速度を表しており,この条件は波長πΔの水面波に対するCFL条件と解釈できる.最小の波長は2Δであり,最小の波長の伝播を解像できなくとも,計算が安定になることがわかる.この理由は,後述するように,離散化の影響により,水面波の伝播速度が遅れるからと考えられる.
以上の結果は水面波の計算の際に,時間刻みΔtを決定する上で重要な目安となる.
なお,粘性がある場合でも,波の伝播速度はわずかに小さくなるだけであるので,粘性の影響は考慮する必要はない.
位相誤差
この項では,数値計算で水面波を計算した際に,波の位相が差分近似によってどのような影響を受けるか検討する.前節で定義されたαを,
とおくと,
である.計算の安定条件は,すべての波数に対して,θ_αが存在するために条件でもあ
る.θ_αは時間を1ステップ計算を進めた際に波数kの波に加わる位相である.角振動数σは単位時間あたりに変化する位相なので,
となる.βの場合も同様である.
離散化されていない時の角振動数
と比較すると,低波数の領域では角振動数は互いに一致しているが,高波数では離散化によって位相が遅れ,角振動数が小さくなる.高波数の波の挙動が重要となる計算では,位相誤差が計算結果に影響を及ぼす可能性がある.
とおくと,
である.計算の安定条件は,すべての波数に対して,θ_αが存在するために条件でもあ
る.θ_αは時間を1ステップ計算を進めた際に波数kの波に加わる位相である.角振動数σは単位時間あたりに変化する位相なので,
となる.βの場合も同様である.
離散化されていない時の角振動数
と比較すると,低波数の領域では角振動数は互いに一致しているが,高波数では離散化によって位相が遅れ,角振動数が小さくなる.高波数の波の挙動が重要となる計算では,位相誤差が計算結果に影響を及ぼす可能性がある.































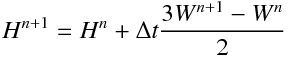





0 件のコメント:
コメントを投稿